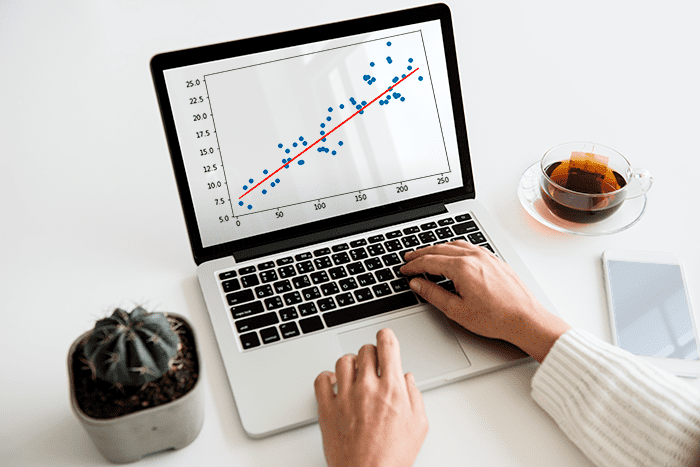
Dalam analisis data, regresi linear adalah salah satu metode yang paling umum digunakan untuk memodelkan hubungan antara variabel independen (variabel prediktor) dan variabel dependen (variabel respons). Metode ini memungkinkan kita untuk memahami dan memprediksi bagaimana perubahan dalam variabel prediktor akan mempengaruhi variabel respons. Dalam artikel ini, kita akan menjelajahi konsep dasar regresi linear, bagaimana metode ini diterapkan dalam analisis data, dan pentingnya dalam pemodelan statistik.
Apa itu Regresi Linear?
Regresi linear adalah metode statistik yang digunakan untuk memodelkan hubungan linier antara satu atau lebih variabel prediktor dengan satu variabel dependen. Dalam regresi linear sederhana, hanya ada satu variabel prediktor yang digunakan untuk memprediksi variabel dependen. Namun, dalam regresi linear berganda, lebih dari satu variabel prediktor digunakan.
Konsep Dasar Regresi Linear
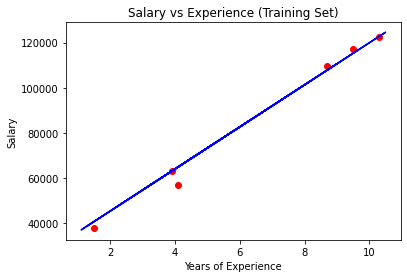
Regresi linear didasarkan pada asumsi bahwa hubungan antara variabel prediktor dan variabel dependen dapat dijelaskan menggunakan persamaan garis lurus. Dalam regresi linear sederhana, persamaan umumnya diberikan oleh:
Y = a + bX
- Y merupakan variabel dependen yang akan diprediksi.
- X adalah variabel prediktor (variabel independen) yang digunakan untuk memprediksi Y.
- a disini merupakan intercept, apabila nilai Y ketika X = 0.
- b adalah koefisien regresi, yang menggambarkan perubahan dalam nilai Y ketika X berubah satu unit.
Jenis-jenis Regresi Linear
Terdapat beberapa jenis regresi linear yang sering digunakan tergantung pada jumlah variabel independen yang digunakan dalam model. Beberapa jenis regresi linear yang umum meliputi:
1. Regresi Linear Sederhana
Regresi linear sederhana merupakan jenis regresi linear yang menggunakan satu variabel independen untuk memprediksi variabel dependen. Persamaan regresi linear sederhana dijelaskan pada rumus dibawah ini.
Y = a + bX
Contohnya, jika kita ingin memprediksi harga rumah berdasarkan luas tanah, kita dapat menggunakan regresi linear sederhana dengan luas tanah sebagai variabel independen dan harga rumah sebagai variabel dependen.
2. Regresi Linear Berganda
Regresi linear berganda digunakan ketika terdapat lebih dari satu variabel independen yang digunakan untuk memprediksi variabel dependen. Persamaan regresi linear berganda dijelaskan pada rumus dibawah ini.
Y = a + b1 X1 + b2 X2 + …. + bn Xn.
Misalnya, jika kita ingin memprediksi pendapatan seseorang berdasarkan usia, pendidikan, dan pengalaman kerja, kita dapat menggunakan regresi linear berganda dengan usia, pendidikan, dan pengalaman kerja sebagai variabel independen dan pendapatan sebagai variabel dependen.
Langkah-langkah dalam Analisis Regresi Linear

Untuk melakukan analisis regresi linear, terdapat beberapa langkah yang harus diikuti:
1. Kumpulkan Data
Langkah pertama adalah mengumpulkan data untuk variabel dependen dan variabel independen yang ingin digunakan dalam analisis regresi linear. Data ini dapat diperoleh melalui survei, pengukuran, atau sumber data lainnya.
2. Analisis Data
Setelah data terkumpul, langkah selanjutnya adalah menganalisis data untuk memahami hubungan antara variabel dependen dan variabel independen. Ini dapat dilakukan dengan menggunakan teknik visualisasi data seperti diagram pencar (scatter plot) atau menggunakan metode statistik seperti korelasi.
3. Membuat Model Regresi Linear
Setelah hubungan antara variabel dependen dan variabel independen telah dipahami, langkah berikutnya adalah membuat model regresi linear. Model ini akan menggambarkan hubungan matematis antara variabel dependen dan variabel independen.
4. Melakukan Estimasi Koefisien Regresi
Setelah model regresi linear dibuat, langkah selanjutnya adalah melakukan estimasi koefisien regresi (β0, β1, β2, dst.). Estimasi ini dilakukan dengan menggunakan teknik seperti Metode Kuadrat Terkecil (Least Squares Method).
5. Evaluasi Model
Setelah estimasi koefisien regresi dilakukan, langkah terakhir adalah mengevaluasi model regresi linear yang telah dibuat. Evaluasi ini melibatkan pengujian asumsi-asumsi model, seperti asumsi normalitas dan homoskedastisitas.
Kesimpulan
Regresi linear adalah metode statistik yang kuat dan umum digunakan untuk memodelkan hubungan antara variabel prediktor dan variabel dependen. Dalam analisis data, regresi linear membantu kita memahami dan memprediksi bagaimana perubahan dalam variabel prediktor akan mempengaruhi variabel dependen. Dengan mengikuti langkah-langkah analisis regresi linear yang tepat, kita dapat menghasilkan model yang dapat digunakan untuk membuat prediksi yang berharga.